DOWNLOAD PDF

In a previous article, we listed DAX pillars and noted that the list is pretty short. Still, those few items are so important that we here have a practical case where, if you do not take the right road immediately, the lack of knowledge in one of those pillars will cause you a big headache.

We shall now outline you a the challenge of a calculated column, show you the simplest possible DAX code to solve it (no puzzle there) and then show you how difficult the same calculated column can become if you take the wrong road, due to the fact that, in the wrong road, you are colliding with one of the pillars.

So this is going to be useful to show you what NOT to do again (like we did in this article) but, at the same time, to challenge you in understanding what the issue is on the wrong road and solve it (let us consider this as a DAX puzzle to solve, not a useful technique).

Should you take the wrong road, we want you to be able to solve but, please, try also to understand why the road is wrong so you take the right (and simpler) one in the future. The DAX code should always be the simplest possible.

The model used is a simple star schema shown in figure 1.

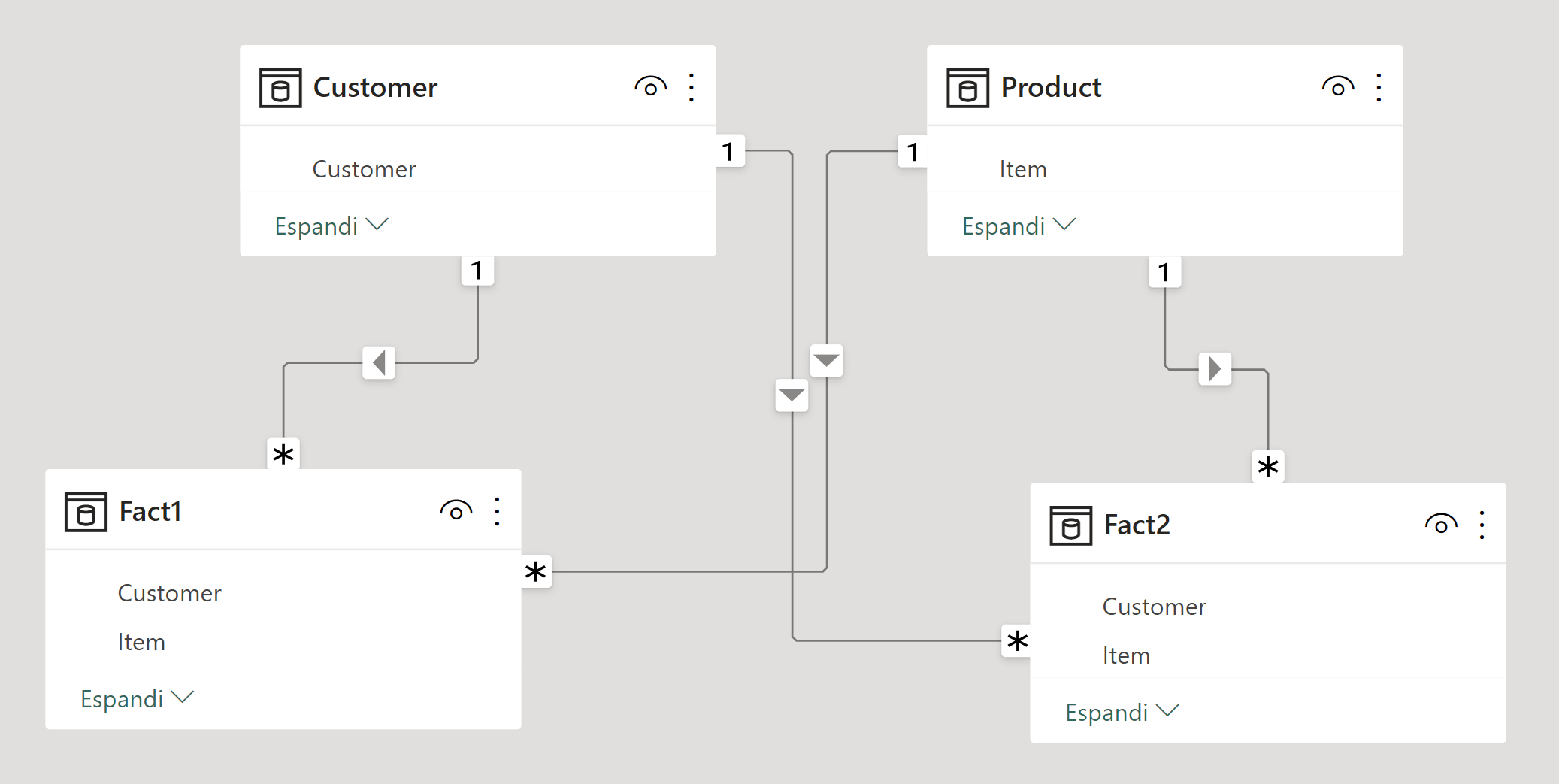
Figure 1

In the following figures you can observe the two fact tables, Fact1 (figure 2) and Fact2 (figure 3).

 

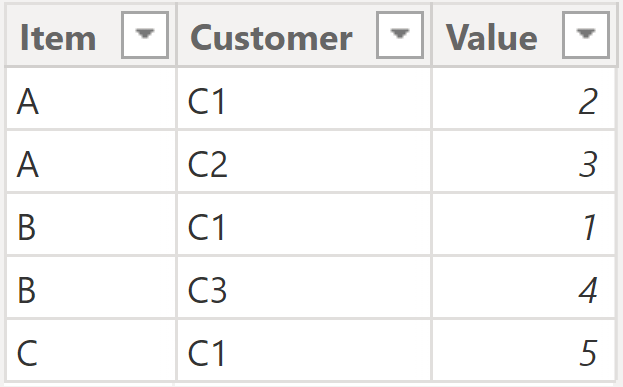
Figure 2

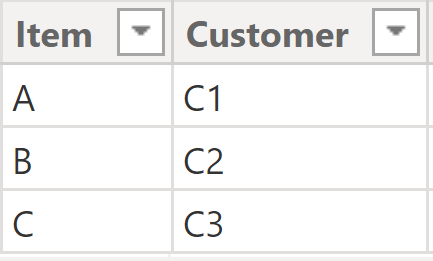
Figure 3

Now the challenge: a calculated column is needed, on Fact2, that shows the minimum value of the Fact1[Value] column for the Item in the current row of Fact2 (Fact2[Item]). Notice that Fact2[Item] is a primary key.

 

Discussion

First things first. The best solution to this problem is a pretty simple DAX formula, here below shown.

Min Fact1 Value MINX =
VAR Fact2Item = Fact2[Item]
RETURN
    MINX (
        FILTER (
            Fact1,
            Fact1[Item] = Fact2Item
        ),
        Fact1[Value]
    )

The above DAX formula solves the problem as you can see in figure 4.

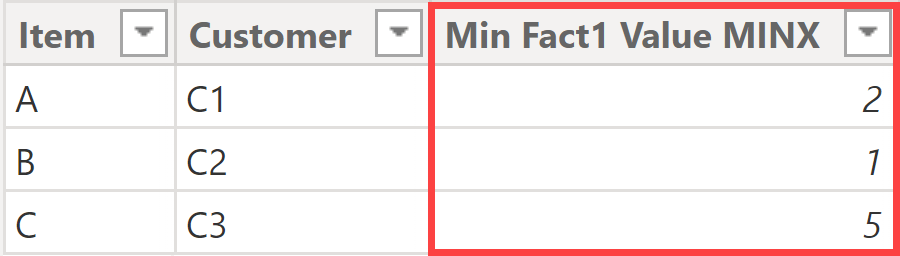
Figure 4

Anyway, it might happen that you take another (and bad) road, using CALCULATE. In this case, the first attempt might look like this (again notice that Fact2 has a primary key, so it is allowed to take advantage of context transition).

Min Fact1 Value CALCULATE =
CALCULATE (
    MIN ( Fact1[Value] )
)

Anyway, this code does not work as you can see in the following figure.

Figure 5

Should it have worked, though? Well, apparently the answer is no: here is why.

The CALCULATE algorithm has five steps:

1.       evaluation of the filters in the outer filter context (there are no filters here);

2.     context transition;

3.     application of the global modifiers (there are none here);

4.     application of the step-1 filters (again there are no filters);

5.     evaluation of the first CALCULATE argument ( MIN ( Fact1[Value] ).

Out of the five steps, therefore, only step 2 and step 5 take place. What is the effect of the context transition on the Fact2 table? The initially empty filter context is now filled with two filters. If we consider the first row of Fact2, these filters are: Fact2[Item] = “A” and Fact2[Customer] = “C1”. Do these filters propagate anywhere? Again apparently, the answer is no (check figure 1) as a filter applied on Fact2 does not seem to propagate anywhere. Therefore, we should have expected a column resulting in the same value on every row: the minimum value of the Fact1[Value] column, namely 1.

BUT… We do have a different result on the first row (see figure 5, the result is 2) and blank on the other two rows. So something else is happening, and in any case we do not get neither the expected result nor the desired one.

Why?

Here is the importance of pillars. One of the pillars of DAX is the expanded table theory: one of its principles is that context transition happens on the expanded table version of Fact2, which contains not only Fact2 columns but also all the columns of all the tables having a one-to-many relationship with Fact2, namely Product and Customer. Therefore, after context transition happens, the filter context contains more filters than we thought. The additional filters are on the columns of both Product and Customer. Let us take a look at those two tables.

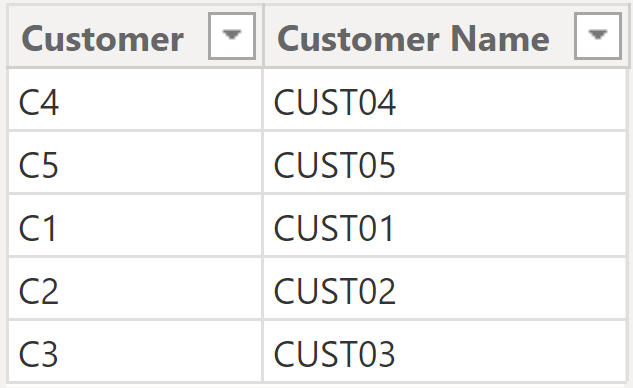
Figure 6

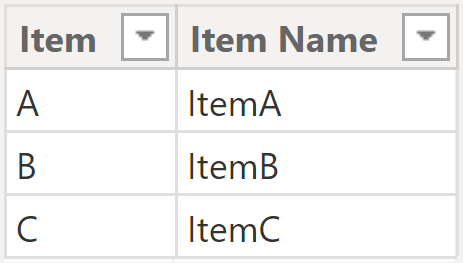
Figure 7

Let us again consider the first row of Fact2. The filters Fact2[Item] = “A” and Fact2[Customer] = “C1” are not alone in the filter context. There will be, in addition, the following filters: Customer[Customer] = “C1”, Customer[Customer Name] = “CUST01”, Product[Item] = “A” and, finally, Product[Item Name] = “ItemA”.

Do any of these filters propagate anywhere? Yes, indeed: those belonging to Product and Customer will propagate to Fact1. So, Fact1 will only show rows in which Fact1[Item] = “A” and Fact1[Customer] = “C1”. There is only one row in Fact1 with these characteristics, the first one. In that row, Fact1[Value] = 2 and that is the reason we get that number as a result on the first row of Fact2. Therefore, that result is not strictly “correct”, it is by chance we got an apparently correct result on that row.

What about the other two rows of Fact2, in which we get BLANK? Well, again, let us consider the filter context after context transition. Filters will be: Fact2[Item] = “B”, Fact2[Customer] = “C2”, Customer[Customer] = “C2”, Customer[Customer Name] = “CUST02”, Product[Item] = “B” and, finally, Product[Item Name] = “ItemB”. Again, the filters belonging to Product and Customer will propagate to Fact1. Point is that, on Fact1, there are no rows with Fact1[Item] = “B”, Fact1[Customer] = “C2”, so the result is an empty table and the calculation returns a blank value. Same reasoning for the third row of Fact2.

OK, so now we know the issue. We also know this is a bad road taken as there is a simpler way to solve. But let us solve the problem on the bad road just to test our knowledge of DAX. Can we get the right result using CALCULATE? Yes, we can. We just have to get rid of the filters, created by context transition, that we do not want.

We do want the filter on Product[Item] but we do not want the filter on Customer[Customer]. So the right code for our calculated column will be the following.

 

Min Fact1 Value CALCULATE =
CALCULATE (
    MIN ( Fact1[Value] ),
    REMOVEFILTERS ( Customer )
)

The above code solves the problem as you can see in the following figure.

Figure 8

Conclusions

DAX pillars can give you a headache if you do not know them in particularly complex cases or when you take the wrong road on relatively simple problems like the one we just solved. It makes sense to know pillars, but the most important thing is avoiding taking advantage of them complicating things. Give priority to the simplest possible solution of any DAX problem and, by the way, be sure to be confident with all DAX pillars!

DOWNLOAD PDF